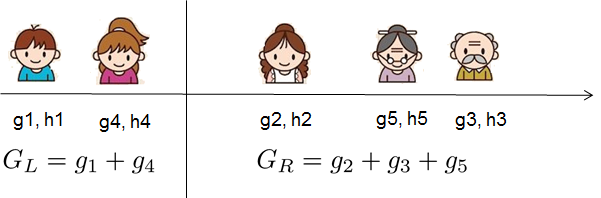2019/01/24 14:07

XGBoost入门系列第一讲

Boosted Trees 介绍

XGBoost 是 “Extreme Gradient Boosting”的简称，其中“Gradient Boosting”来源于附录1.Friedman的这篇论文。本文基于 gradient boosted tree ，中文可以叫梯度提升决策树，下面简称GBDT，同时也有简称GBRT，GBM。针对gradient boosted tree的细节也可以参考附录2.这篇网页，感兴趣的朋友可以前往BigQuant进一步学习实践。

监督学习

XGBoost 主要是用来解决有监督学习问题，此类问题利用包含多个特征的训练数据 $x_{i}$ ，来预测目标变量 $y_{i}$ 。在我们深入探讨GBDT前，我们先来简单回顾一下监督学习的一些基本概念。

模型与参数

在监督学习中模型（model）表示一种数学函数，通过给定 $x_{i}$ 来对 $y_{i}$ 进行预测。以最常见的线性模型（linear model）举例来说，模型可以表述为 $\hat{y_{i}} = \sum_{j} θ_{j} x_{i j}$ ，这是一个输入特性进行线性加权的函数。那么针对预测值的不同，可以分为回归或者分类两种。
在监督学习中参数（parameters）是待定的部分，我们需要从数据中进行学习得到。在线性回归问题中，参数用 $θ$ 来表示。

目标函数：训练误差 + 正则化

根据对 $y_{i}$ 的不同理解，我们可以把问题分为，回归、分类、排序等。我们需要针对训练数据，尝试找到最好的参数。为此，我们需要定义所谓的目标函数，此函数用来度量参数的效果。
这里需要强调的是，目标函数必须包含两个部分：训练误差和正则化。

其中， $L$ 表示训练误差函数， $Ω$ 表示正则项。训练误差用来衡量模型在训练数据上的预测能力。比较典型的有用均方差来衡量。

另外针对逻辑回归，比较常见的损失函数为Logistic函数：

另外一个比较重要的部分就是正则项，这也是很多人容易忘记的部分。正则项是用来控制模型的复杂度，以防止过拟合（overfitting）。这听起来有点抽象，那么我们用下面的例子来说明。针对下面左上角的这幅图，我们需要找到一个阶梯函数来拟合图中的数据点集合。那么问题来了，下面剩下的三幅图中，哪一个你认为是最好的呢？

答案是用红色标注出来的这幅图。为什么呢？因为我们对于好的模型的判断依据是简单（simple）并且准确（predictive）。但这两者又是相互矛盾的，在机器学习中我们也把这两者也用 bias-variance 来表述。

复合树模型（Tree Ensemble）

在前面我们已经介绍了监督学习，现在让我们开始了解树模型。首先先来了解一下xgboost所对应的模型：复合树模型。复合树模型是一组分类和回归树（classification and regression trees - CART）。这里我们举CART中的一个例子，一类分类器用来辨别某人是否喜欢计算机游戏。

我们把家庭中的成员分到了不同的叶子节点，同时每个叶子节点上都有一个分数。CART与决策树相比，细微差别在于CART的叶子节点仅包含判断分数。在CART中，相比较于分类结果，每个叶子节点的分数给我们以更多的解释。这让CART统一优化节点更为容易，这在后面会有具体介绍。

通常情况下，在实践中往往一棵树是不够用的。这个时候往往需要把多棵树的预测结果综合起来，这就是所谓的复合树模型。

上面就是由两棵树组成的复合树的例子。每棵树上的分数简单相加就得到了最终的分数。用数学式子可以表达如下：

$K$ 表示树的数目， $f$ 是函数空间 $F$ 中的一个函数， $F$ 表示CART的所有可能集合。所以我们的优化目标可以写作：

现在问题来了，随机森林对应的模型是什么呢？对了，也是复合树模型。所以在模型的表述上，随机森林和提升树是一样的，他们俩的区别只是在于如何训练。这也就意味着，如果要写一个关于复合树模型的预测服务，我们只需要写一个就可以同时支持随机森林和提升树。

提升树（Tree Boosting）

介绍了模型之后，让我们看看训练部分。那么我们是怎么训练这些树的呢？对于所有的监督学习模型，答案也都是同样，只需要做两件事，定义目标函数，然后优化它。
假设我们有如下的目标函数（需要切记目标函数必须包含损失函数及正则项）

增量训练（Additive Training）

首先我们需要问的是，这些树的参数是什么？我们会发现，我们所要学习的就是这些 $f_{i}$ 方法，每个方法中定义树的结构以及叶子节点的分数。这比传统最优化问题要更难，传统最优化问题我们可以通过梯度来解决。而且我们无法在一次训练所有的树。相反，我们用增量（additive）的方式：每一步我们都是在前一步的基础上增加一棵树，而新增的这棵树是为修复上一颗树的不足。，我们把每 $t$ 步的预测用 ${\hat{y_{i}}}^{(t)}$ 表示，这样我们就有了：

这里还有疑问的是，在每一步中如何确定哪棵树是我们需要的呢？一个很自然的想法就是，增加这棵树有助于我们的目标函数。

我们用MSE（均方差）作为损失函数，这样式子就变成了：

对于用MSE求出来的损失函数式子比较友好，包含一个一阶项和一个二次项。但是对于其他形式，就很难推导出这么友好的损失函数式子了。那么针对这种情形，我们就用泰勒展开公式（参考附录4， $x$ 取值 ${\hat{y_{i}}}^{(t - 1)} + f_{t} (x_{i})$ ， $a$ 取值 ${\hat{y_{i}}}^{(t - 1)}$ ）来逼近：

其中 $g_{i}$ 和 $h_{i}$ 定义如下：

然后针对上述式子，我们删除常数项，那么在 $t$ 目标函数就变成：

选择新的一棵树，上述式子就是优化目标。这样的优化目标有一个优点，式子只需要考虑 $g_{i}$ 和 $h_{i}$ 。这就是xgboost为什么能支持自定义损失函数的原因。我们能够优化每一个损失函数，包括逻辑回归和加权逻辑回归，只需要把对应的 $g_{i}$ 和 $h_{i}$ 作为输入传入即可。

模型复杂度

现在讲讲正则化。那么如何定义 $Ω (f)$ 呢，在此之前，我们需要定义 $f (x)$ ：

这里 $w$ 表示叶子节点上的分数所组成的向量， $q$ 表示每个数据映射到相应叶子节点的对应关系函数， $T$ 表示叶子节点的数量。在XGBoost中，我们用如下公式定义复杂度：

当然还有其他公式来定义复杂度，但是我们发现上述式子在实践过程中表现很好。其他树相关的算法包不怎么认真对待正则化，甚至直接忽视掉。

如何计算树叶子节点上的分数

那么在增量学习过程中，如何选择这棵新增的树呢？要解决这个问题，我们先解决一下其中这个子问题：假设这棵树的结构已经确定了，如何来计算叶子节点上的分数？
这一部分是推广过程中比较神奇的一个步骤。根据上述过程，我们写出第 $t$ 步树的目标值：

这里 $I_{j} = i | q (x_{i}) = j$ 表示每个映射到第 $j$ 个叶子节点对应的数据样本。需要注意的是，因为映射到相同叶子节点上的数据样本他们的分数是相同的，所以在第二行我们改变了一下求和 $\sum$ 顺序。同时我们令 $G_{j} = \sum_{i \in I_{j}} g_{i}$ 以及 $H_{j} = \sum_{i \in I_{j}} h_{i}$ ，那么上述公式简化为：

在上述式子中，每一个 $w_{j}$ 是相互独立的，那么针对一元二次方程 $G_{j} w_{j} + \frac{1}{2} (H_{j} + λ) w_{j}^{2}$ 而言，可以比较容易求出当新增的这棵树的结构 $q (x)$ 已知的情况下，目标函数最小值下的 $w_{j}$ ：

最后的式子计算的是树 $q (x)$ 的优劣：

如果上面的式子看着比较复杂的话，那么根据上面的这幅图来看如何计算这些分数，就会显得更直观些。一旦树的结构已知的话，我们只需要通过计算每个节点上的 $g_{i}$ 和 $h_{i}$ ，然后把各个叶子节点上的这些数值加起来，用上述方程式就可以计算这棵树的优劣了。

如何学习树的结构

现在我们已经知道一旦树的结构固定下来以后，如何来计算叶子节点上的分数，以及计算这棵树的优劣。那么关于现在我们要来解决如何来学习这棵树的结构。比较简单粗暴的方法就是遍历所有可能的树结构，然后从中找到最好的那棵树。但是这也是不切实际的，因为需要遍历的情况实在是太多了。所以我们来寻求一种贪婪的解法，就是在树的每个层构建的过程中，来优化目标。那么这里假设在某一层的构建过程中，假设特征已经选定，我们先如何进行二叉划分呢，以及是不是需要进行划分？我们可以通过下面的式子来计算划分之后，在目标上所获得的收益（这个收益越越好，负数表示收益为负）：

上面的这个式子可以分解为 1) 若是划分，划分后左边节点的收益 2) 或是划分，划分后右边节点的收益 3) 如不划分，原先节点的收益 4) 划分后正则项的收益。通过上述式子比较容易看到，当划分后叶子节点所带来的新增收益小于 $γ$ ，我们最好还是不要进行二叉划分，保留原样是最好的。这也是日后做剪枝的依据。

那么针对排序后的特征，我们所要做的就是遍历各种划分，找到一个最好的划分点，如下图表示。

那么这里还有一个问题就是在构建树的结构过程中，在某一层如何进行特征选择呢？这里提供了一种比较简单的方式就是遍历每一种特征，然后根据上述式子的Gain，找到最大的Gain值对应的特征。

关于XGBoost的最后几句话

我们花了很长时间来讲解 Boosted Tree，那么XGBoost相较于Boosted Tree，又做了哪些额外的事情呢？XGBoost是遵循上述Boosted Tree思想的工程实现，但同时又考虑兼顾系统优化和机器学习原理，最大化的保证可扩展性、便捷性以及准确性。

附录：

《Greedy Function Approximation: A Gradient Boosting Machine》
http://www.csuldw.com/2015/08/19/2015-08-19%20GBDT/
https://xgboost.readthedocs.io/en/latest/model.html
https://zh.wikipedia.org/wiki/泰勒公式
http://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf

原文链接：《 XGBoost 入门系列第一讲》

本文由BigQuant人工智能量化投资平台原创推出，版权归BigQuant所有，转载请注明出处。

宽邦科技

提供金融行业人工智能平台和服务解决方案，研发了全国首个人工智能量化投资平台BigQuant，拥有全栈人工智能平台和大规模机器学习和深度学习框架与算法，为券商、银行、保险、资管等金融机构以及更多企业提供AI技术方案和业务解决方案，实现机构及企业的AI转型和升级。

入门XGBoost机器学习监督学习目标函数

相关数据

增量学习技术

增量学习作为机器学习的一种方法，现阶段得到广泛的关注。对于满足以下条件的学习方法可以定义为增量学习方法： * 可以学习新的信息中的有用信息 * 不需要访问已经用于训练分类器的原始数据 * 对已经学习的知识具有记忆功能 * 在面对新数据中包含的新类别时，可以有效地进行处理

来源：Polikar R, Upda L, Upda S S, et al. Learn++: An incremental learning algorithm for supervised neural networks Wikipedia

逻辑回归技术

逻辑回归（英语：Logistic regression 或logit regression），即逻辑模型（英语：Logit model，也译作“评定模型”、“分类评定模型”）是离散选择法模型之一，属于多重变量分析范畴，是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。

来源：Trevor Hastie, Robert Tibshirani and Jerome Friedman (2nd ed., 2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction.维基百科

机器学习技术

机器学习是人工智能的一个分支，是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科。机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。因为学习算法中涉及了大量的统计学理论，机器学习与推断统计学联系尤为密切，也被称为统计学习理论。算法设计方面，机器学习理论关注可以实现的，行之有效的学习算法。

来源：Mitchell, T. (1997). Machine Learning. McGraw Hill.

人工智能技术

在学术研究领域，人工智能通常指能够感知周围环境并采取行动以实现最优的可能结果的智能体（intelligent agent）

来源：Russell, S., & Norvig, P. (2003). Artificial Intelligence: A Modern Approach.

参数技术

在数学和统计学裡，参数（英语：parameter）是使用通用变量来建立函数和变量之间关系（当这种关系很难用方程来阐述时）的一个数量。

来源：维基百科

剪枝技术

剪枝顾名思义，就是删去一些不重要的节点，来减小计算或搜索的复杂度。剪枝在很多算法中都有很好的应用，如：决策树，神经网络，搜索算法,数据库的设计等。在决策树和神经网络中，剪枝可以有效缓解过拟合问题并减小计算复杂度；在搜索算法中，可以减小搜索范围，提高搜索效率。

来源：Wikipedia

梯度提升技术

梯度提升是用于回归和分类问题的机器学习技术，其以弱预测模型（通常为决策树）的集合的形式产生预测模型。它像其他增强方法一样以阶段式方式构建模型，并且通过允许优化任意可微损失函数来推广它们。

来源：Wikipedia

损失函数技术

在数学优化，统计学，计量经济学，决策理论，机器学习和计算神经科学等领域，损失函数或成本函数是将一或多个变量的一个事件或值映射为可以直观地表示某种与之相关“成本”的实数的函数。

来源：Wikipedia

运筹优化技术

最优化问题（英语：Optimization problem）在数学与计算机科学领域中，是从所有可行解中寻找最优良的解的问题。根据变数是连续的或离散的，最佳化问题可分为两类：连续最佳化问题与组合优化。

来源：Wikipedia

随机森林技术

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。 Leo Breiman和Adele Cutler发展出推论出随机森林的算法。而"Random Forests"是他们的商标。这个术语是1995年由贝尔实验室的Tin Kam Ho所提出的随机决策森林（random decision forests）而来的。这个方法则是结合Breimans的"Bootstrap aggregating"想法和Ho的"random subspace method" 以建造决策树的集合。

来源：维基百科

分类和回归树技术

CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征，将输入空间即特征空间划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。

来源：Breiman, Leo; Friedman, J. H., Olshen, R. A., & Stone, C. J. Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. 1984. ISBN 978-0-412-04841-8.Classification and regression trees 李航. (2012). 统计学习方法. 清华大学出版社

线性回归技术

在现实世界中，存在着大量这样的情况：两个变量例如X和Y有一些依赖关系。由X可以部分地决定Y的值，但这种决定往往不很确切。常常用来说明这种依赖关系的最简单、直观的例子是体重与身高，用Y表示他的体重。众所周知，一般说来，当X大时，Y也倾向于大，但由X不能严格地决定Y。又如，城市生活用电量Y与气温X有很大的关系。在夏天气温很高或冬天气温很低时，由于室内空调、冰箱等家用电器的使用，可能用电就高，相反，在春秋季节气温不高也不低，用电量就可能少。但我们不能由气温X准确地决定用电量Y。类似的例子还很多，变量之间的这种关系称为“相关关系”，回归模型就是研究相关关系的一个有力工具。

来源：王松桂等编线性统计模型线性回归与方差分析高等教育出版社 Wikipedia

映射技术

映射指的是具有某种特殊结构的函数，或泛指类函数思想的范畴论中的态射。逻辑和图论中也有一些不太常规的用法。其数学定义为：两个非空集合A与B间存在着对应关系f，而且对于A中的每一个元素x，B中总有有唯一的一个元素y与它对应，就这种对应为从A到B的映射，记作f：A→B。其中，y称为元素x在映射f下的象，记作：y=f(x)。x称为y关于映射f的原象*。*集合A中所有元素的象的集合称为映射f的值域，记作f(A)。同样的，在机器学习中，映射就是输入与输出之间的对应关系。

来源：Wikipedia

监督学习技术

监督式学习（Supervised learning），是机器学习中的一个方法，可以由标记好的训练集中学到或建立一个模式（函数 / learning model），并依此模式推测新的实例。训练集是由一系列的训练范例组成，每个训练范例则由输入对象（通常是向量）和预期输出所组成。函数的输出可以是一个连续的值（称为回归分析），或是预测一个分类标签（称作分类）。

来源：Wikipedia

逻辑技术

人工智能领域用逻辑来理解智能推理问题；它可以提供用于分析编程语言的技术，也可用作分析、表征知识或编程的工具。目前人们常用的逻辑分支有命题逻辑（Propositional Logic ）以及一阶逻辑（FOL）等谓词逻辑。

来源：机器之心

目标函数技术

目标函数f(x)就是用设计变量来表示的所追求的目标形式，所以目标函数就是设计变量的函数，是一个标量。从工程意义讲，目标函数是系统的性能标准，比如，一个结构的最轻重量、最低造价、最合理形式；一件产品的最短生产时间、最小能量消耗；一个实验的最佳配方等等，建立目标函数的过程就是寻找设计变量与目标的关系的过程，目标函数和设计变量的关系可用曲线、曲面或超曲面表示。

来源：百度百科

过拟合技术

过拟合是指为了得到一致假设而使假设变得过度严格。避免过拟合是分类器设计中的一个核心任务。通常采用增大数据量和测试样本集的方法对分类器性能进行评价。

来源：Wikipedia

正则化技术

当模型的复杂度增大时，训练误差会逐渐减小并趋向于0；而测试误差会先减小，达到最小值后又增大。当选择的模型复杂度过大时，过拟合现象就会发生。这样，在学习时就要防止过拟合。进行最优模型的选择，即选择复杂度适当的模型，以达到使测试误差最小的学习目的。

来源：李航著统计学习方法清华大学出版社

特征选择技术

在机器学习和统计学中，特征选择（英语：feature selection）也被称为变量选择、属性选择或变量子集选择。它是指：为了构建模型而选择相关特征（即属性、指标）子集的过程。

来源：维基百科

XGBoost技术

XGBoost是一个开源软件库，为C ++，Java，Python，R，和Julia提供了渐变增强框架。它适用于Linux，Windows，MacOS。从项目描述来看，它旨在提供一个“可扩展，便携式和分布式的梯度提升（GBM，GBRT，GBDT）库”。除了在一台机器上运行，它还支持分布式处理框架Apache Hadoop，Apache Spark和Apache Flink。由于它是许多机器学习大赛中获胜团队的首选算法，因此它已经赢得了很多人的关注。

来源：Wikipedia