在我重新抱起概率统计的课本之前，我一直都不清楚似然函数为什么是那样子的，只知道照着公式敲代码（那时候还没有tensorflow），于是出过各种糗：
“啊？似然函数不就是交叉熵吗？”
“机器学习中的似然函数怎么看起来跟概率统计课本里的不一样呢？”
“学长学长，我把这个model的输出接上交叉熵后怎么报错了？”
“似然函数”名字的意义已经在以前的多篇文章中提过了，更通用的定义来说，似然函数就是衡量当前模型参数对于已知样本集的解释情况，通用的表现形式如下：
注意！似然函数的定义当然没有限定样本集X的分布函数。这样来看似然函数的话很抽象，不知道实际中如何去用。所以我们把问题缩小一下啦。
比如，我们将似然函数作为机器学习模型的损失函数，并且用在分类问题中。
这时，似然函数是直接作用于模型的输出的（损失函数就是为了衡量当前参数下model的预测值predict距离真实值label的大小，所以似然函数用作损失函数时当然也是为了完成该任务），所以对于似然函数来说，这里的样本集就成了label集（而不是机器学习意义上的样本集X了），这里的参数也不是机器学习model 的参数，而是predict值！（哈？是不是觉得搞siao了~屏住呼吸，慢慢来）
其实作为损失函数的似然函数并不关心你当前的机器学习model的参数是怎样的，毕竟它此时所接收的输入只有两部分：1、predict。2、label。当然还有一个隐含的输入——3、分布模型。
显然这里的label就是似然函数手里的观测值，也就是它眼里的样本集。而它眼里的模型，当然就是predict这个随机变量所服从的概率分布模型。它的目的，就是衡量predict背后的模型对于当前观测值的解释程度。而每个样本的predict值，恰恰就是它所服从的分布模型的参数。（好啦，给你1小时的时间理解一下加粗的这几句话，如果理解不了，看下面这个栗子吧）
比如此时我们的机器学习任务是一个4个类别的分类任务，机器学习model的输出就是当前样本X下的每个类别的概率，如predict=[0.1, 0.1, 0.7, 0.1]，而该样本的标签是类别3，表示成向量就是label=[0, 0, 1, 0]。那么label=[0, 0, 1, 0]就是似然函数眼里的样本，然后我们可以假设predict这个随机变量背后的模型是单次观测下的多项式分布，为什么呢？
在谈多项式分布前，先讲一下二项(式)分布。
在讲二项分布前，先讲一下贝努利分布。
贝努利分布也叫两点分布。贝努利分布可以看成是将一枚硬币（只有正反两个面，代表两个类别）向上扔出，出现某个面（类别）的概率情况，因此其概率密度函数为：
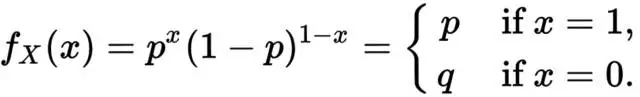
一定要好好体会中间这个 
！！！这是理解似然函数做损失函数的关键！另外，贝努利分布的模型参数就是其中一个类别的发生概率。
而二项分布呢，就是将贝努利实验重复n次（各次实验之间是相互独立的）。
而多项式分布呢，就是将二项分布推广到多个面（类别）。
所以，单次观测下的多项式分布就是贝努利分布的多类推广！即：
其中，C代表类别数。p代表向量形式的模型参数，即各个类别的发生概率，如p=[0.1, 0.1, 0.7, 0.1]，则p1=0.1, p3=0.7等。即，多项式分布的模型参数就是各个类别的发生概率！x代表one-hot形式的观测值，如x=类别3，则x=[0, 0, 1, 0]。xi代表x的第i个元素，比如x=类别3时，x1=0，x2=0，x3=1，x4=0。
好了，聪明的你如果能把这个单次观测下的多项式分布的表达式理解了，那么你就完成80%的理解任务了。
想一下，机器学习model对某个样本的输出，就代表各个类别发生的概率。但是，对于当前这一个样本而言，它肯定只能有一个类别，所以这一个样本就可以看成是一次实验（观察），而这次实验（观察）的结果要服从上述各个类别发生的概率，那不就是服从多项式分布嘛！而且是单次观察！各个类别发生的概率predict当然就是这个多项式分布的参数阿。
好了，建模完成了，小总结一下：
对于多类分类问题，似然函数就是衡量当前这个以predict为参数的单次观测下的多项式分布模型与样本值label之间的似然度。
所以，根据似然函数的定义，单个样本的似然函数即：
所以，整个样本集（或者一个batch）的似然函数即：
(感谢评论区 @Ken Chen 耐心指出这里的错误。之前写成了累加，一直理解错了。今天突然想起来这篇文章好像有读者指出过错误，回来一细想果然错了！原错误公式为，关于该公式为什么错了请见评论区置顶评论。）
看~这就是庐山真面目了。而由于式子里有累乘运算，所以习惯性的加个log函数来将累乘化成累加以提高运算速度（虽然对于每个样本来说只有一个类别，但是哪怕是算0.2^0也是算了一遍指数函数啊，计算机可不会直接口算出1）。所以在累乘号前面加上log函数后，就成了所谓的对数似然函数：
而最大化对数似然函数就等效于最小化负对数似然函数，所以前面加个负号后不就是我们平常照着敲的公式嘛。。。
而这个形式跟交叉熵的形式是一模一样的：
对于某种分布的随机变量X~p(x), 有一个模型q(x)用于近似p(x)的概率分布，则分布X与模型q之间的交叉熵即：
这里X的分布模型即样本集label的真实分布模型，这里模型q(x)即想要模拟真实分布模型的机器学习模型。可以说交叉熵是直接衡量两个分布，或者说两个model之间的差异。而似然函数则是解释以model的输出为参数的某分布模型对样本集的解释程度。因此，可以说这两者是“同貌不同源”，但是“殊途同归”啦。
当然，补充一句无关的话，在将负对数似然/交叉熵拿来做损失函数的时候，不要忘记对batch取average，这样算出来的才是期望（直接套公式出来的是sum版）。
over。
算了，再送点赠品好了~
同样的道理，使用似然函数作为损失函数时，多于多类的情况，很自然的建模出了单次观测下的多项式分布，那么二类情况呢？当然就是前面已经讲过的贝努利分布啦~快点把贝努利分布的概率密度函数带进去试试吧~是不是突然发现，二类分类器逻辑回归的损失函数“pia”的一下就出来啦~
本文转载自【夕小瑶的卖萌屋】，听说每一个想学机器学习的人到这里都停不下来了~
