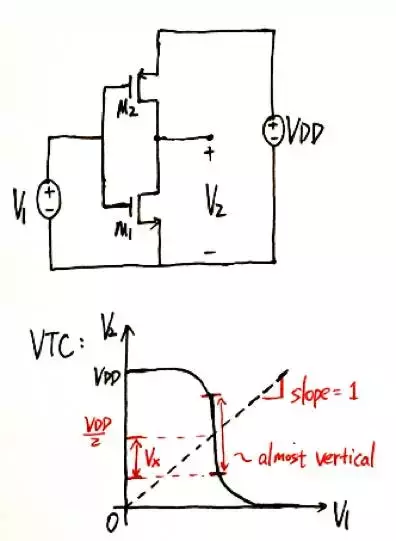
在上一讲(震惊!UCLA电路大佬用的MOS模型竟然不是平方律而是...)中我们给大家介绍了EKV模型的基本概念以及在大信号和小信号分析中的应用。尤其在大信号分析中,EKV图形化的方法简单直观,有着得天独厚的优势。在进入MOSFET不同反型区的推导前,我们首先讲两个例子,教大家如何用EKV模型秒掉拉扎维(的模拟电路面试考题),同时也让大家再次领略EKV模型的威力。
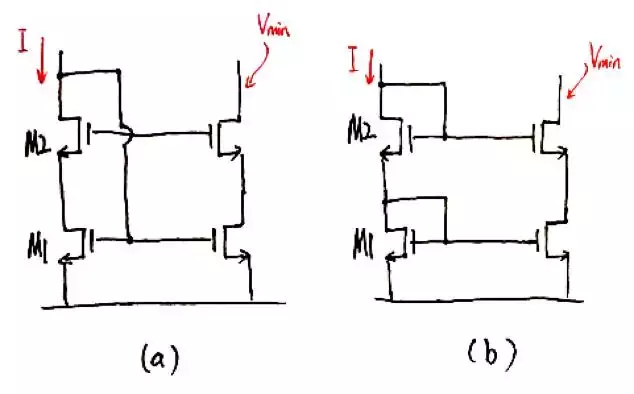
上图所示是两个电流镜电路。对于一个电流镜电路,高输出电阻和高电压裕度(voltageheadroom)是两个重要的指标。由于共源共栅管的存在,两个电路的输出电阻都很大。那么哪个电路的电压裕度更大呢?我们还是通过画三角形的方式来分析。
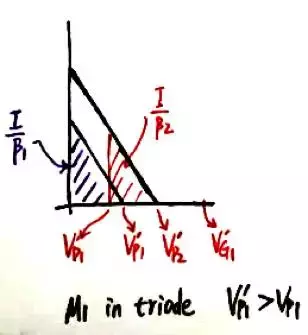
对于(a),为了简化分析,假设M1和M2有相同的(W/L),因而β相同。在下图中的偏置电压下(M2的偏置电路在电路图中未画出),M1和M2都处在饱和状态,由于流过的电路以及β都相同,所以两个三角形的面积相同。外电路的最小电压Vmin=Vp2。
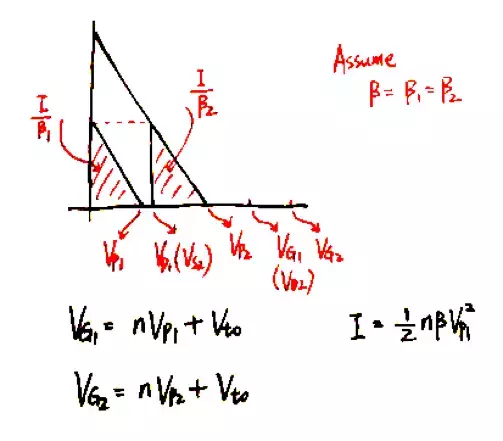
如果逐渐减小M2的偏置电压VG2,右侧的小三角形会随之左移,直至VS2恰好等于VP1,此时为临界偏置点,此时电路有最大的电压裕度:
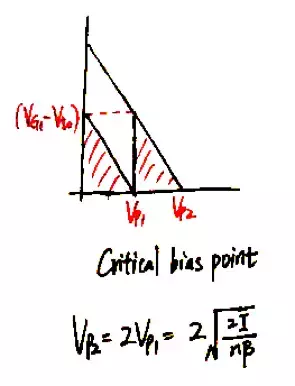
如果继续减小VG2,M1将进入三极管区。由于输入电流恒定,因而代表M1电流的紫色梯形面积和之前的三角形面积相等,所以Vp1会自动增大。
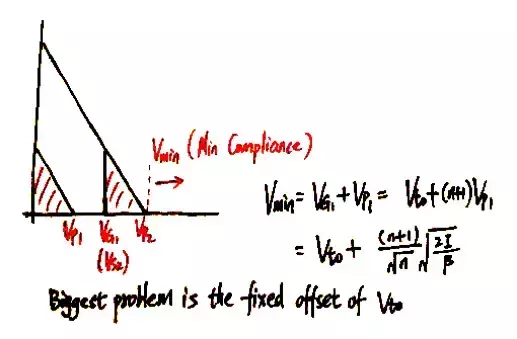
接下来我们分析(b)中的电路,由于VG1=Vs2,从图中可知,Vmin比(a)中的电路大约多出了一个阈值电压的大小。
第二个例子我们尝试用EKV模型来求解拉扎维模电书上的一道习题(第11章习题第一题),题目如下图所示:
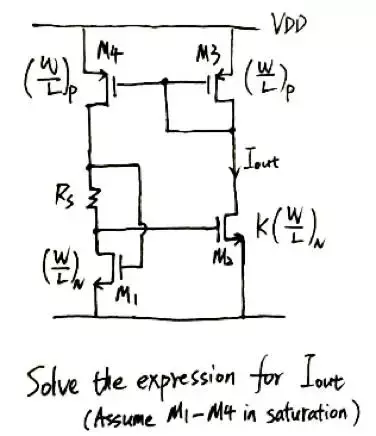
我们先后画出左右两条支路的“三角形”示意图,PMOS电流镜的两个MOS管对应的三角形完全相同,而左边支路的NMOS对应的三角形面积是右边NMOS的K倍,因而左边三角形边长是右边的根号K倍。由此可以轻松地计算出输出电流的表达式。
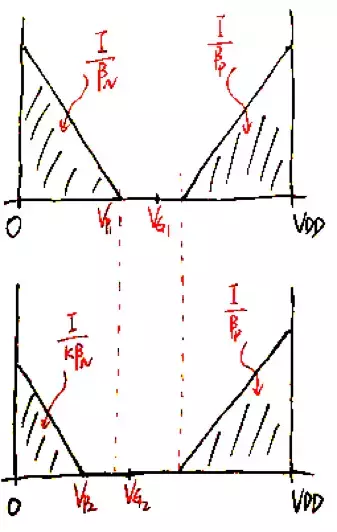
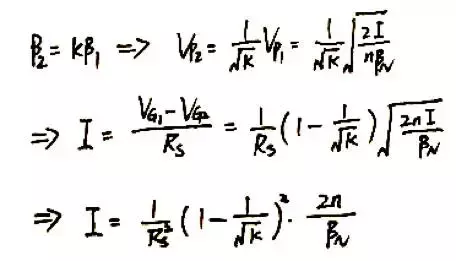
对比拉扎维书的解答,唯一的不同是这里还考虑了体效应因子n(所以如果拉扎维的标准答案是100分使用EKV方法求解的答案应该得120分:))。
反型区模型
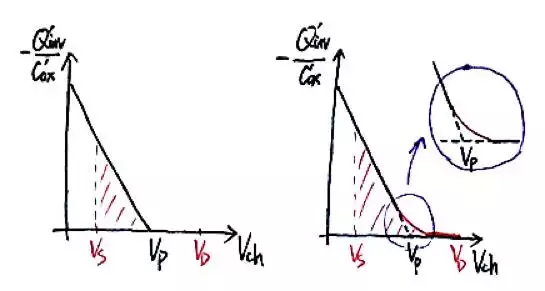
在上一讲中我们提到,EKV模型在强反型区(stronginversion)、中间反型区(moderateinversion)和弱反型区(weakinversion)连续准确。强反型区自然就是大家熟悉的平方率模型,也就是之前反复使用的“三角形”(左图);但实际上,在Vp附近的转折不是突变而是连续的(右图)。
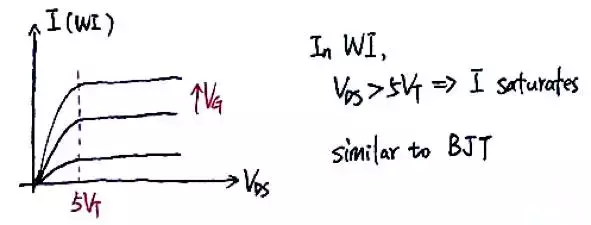
首先我们来简单学习一下弱反型区的模型。MOS管在弱反型区的工作状态和BJT基本相同,扩散电流(diffusioncurrent)占主导,电流和电压之间呈指数关系。

由最后推出的电流公式可知,当VDS大于约5倍的VT时,电流就基本饱和,I-V特性曲线如下图所示:
有了强弱反型区的模型之后,中间反型区的模型可以通过插值公式得到。可以验证,这个公式在强弱反型区均适用。

短沟道效应
讲完了MOS管在不同反型区的模型,接下来我们就谈一谈两个短沟道效应——沟道长度调制效应和速度饱和效应。
(1)沟道长度调制效应
沟道长度调制效应可以说是模拟电路设计中最重要的效应之一,它决定了一个MOS管的输出电阻。如下图所示,在一个MOS管的沟道中,从漏端(D)到源端(S)沟道电压连续下降。如果MOS管处于饱和状态,那么沟道中存在夹断点,该点的沟道电压即为夹断电压(pinch-offvoltage)。夹断点和漏端之间为耗尽区,和源端之间有载流子,这段长度称为有效沟道长度Leff。增大漏端电压VD,夹断点会左移,Leff也会随之减小。
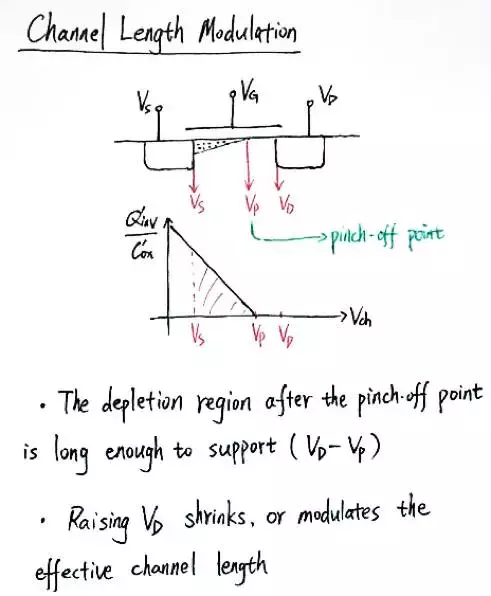
经过推导,我们可以看到MOS管的输出电导go=I/VA=I/(VE*L),通常情况下,VE可以看做一个常数,因而MOS管的输出电阻和沟道长度L成正比,和偏置电路I成反比。

(2)速度饱和效应
我们知道,MOS管沟道的横向电场E= VDS/L,当电场强度较小时,载流子的漂移速度(driftvelocity)v= μ*E,但当漂移速度和电子的热运动速度相近时,这种线性关系就不再成立,漂移速度会趋于饱和。
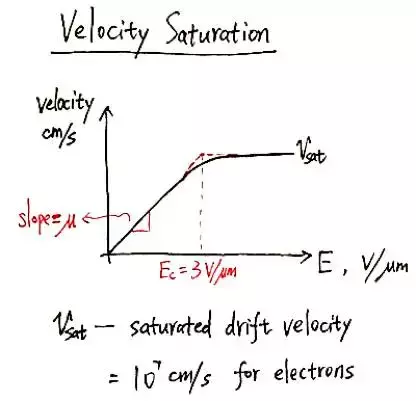
下图中的插值公式同时适用于饱和区和速度饱和区:
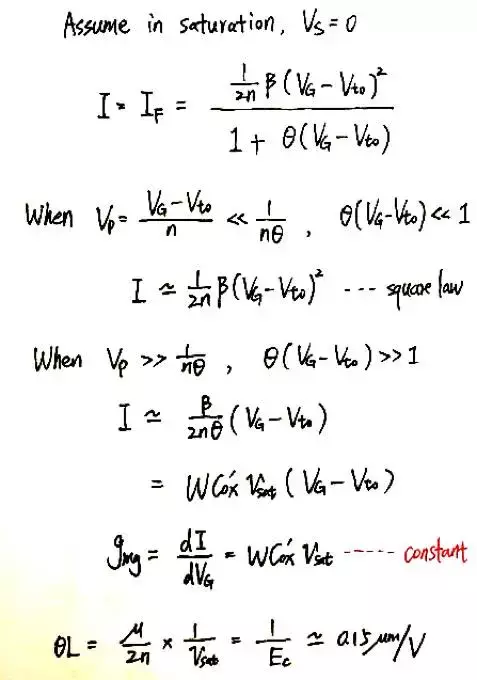

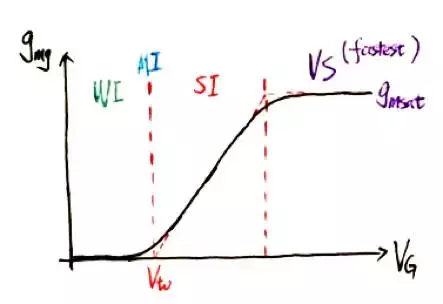
我们来对讲过的内容做一个小小的总结,下图涵盖了MOS管从弱反型区到强反型区再到速度饱和区中gmg的值。在速度饱和区,跨导为一个常数,不再随栅极电压变化。
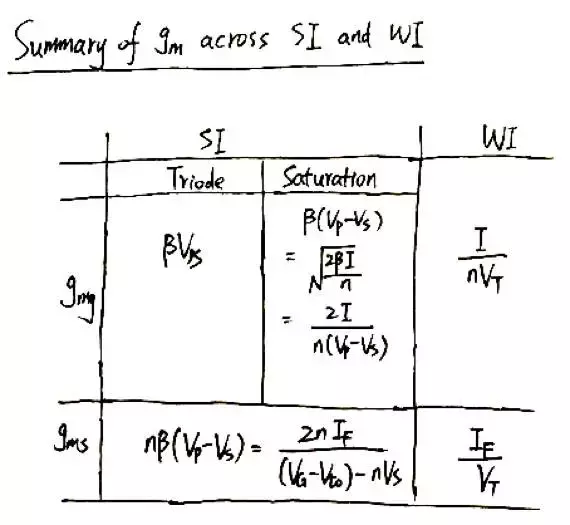
在强反型区和弱反型区的跨导表达式如下表:
在设计中我们通常还会关注一个重要的指标——跨导效率(transconductanceefficiency),即跨导与电流的比值:
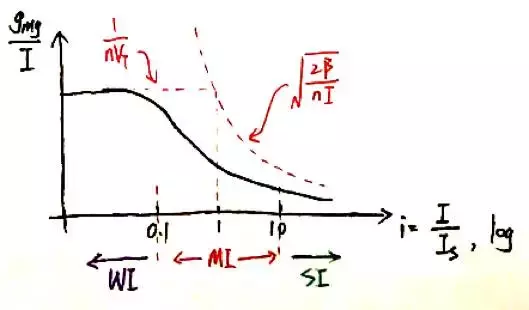
跨导决定了放大器带宽,而跨导效率则决定了达到该带宽需要多少电流。看起来跨导效率是弱反型最好,因此现在许多低功耗设计会把MOSFET偏置在靠近弱反区的地方。然而,在弱反区的噪声,失调(offset)以及大信号性能需要仔细设计,这也是弱反型设计带来的挑战。
最后给大家留一个简单的练习题: