作者：inFERENce
翻译：余志文
去年我一直在研究如何更好地调整GANs中的不足，但因为之前的研究方向只关注了损失函数，完全忽略了如何寻找极小值问题。直到我看到了这篇论文才有所改变：
详解论文: The Numerics of GANs
我参考了Mar的三层分析，并在计算层面上仔细考虑了这个问题：我们这样做的最终目标是什么？我相信GANs在这个层面已经有所突破了，因为他们试图优化错误的东西或寻求不存在的平衡等。这就是为什么我喜欢f-GANs、Wasserstein GANs、实例噪声，而不大喜欢在优化层面上做一些修复的尝试：比如DCGAN或改进技术（Salimans等，2016）等原因。我认为在大多数深度学习中，算法层面上随机梯度的下降是大家所认可的。你可以去提升它，但是如果没有突破性进展，它通常不需要修复。
但阅读本文后，我有一个启示：
GANs可以同时在计算层面和算法层面有所突破
即使我们修复了目标，我们也没有算法工具来寻找实际解决方案。
文章摘要：
结合我目前在研究的内容，我将通过一个不同的视觉来分析该论文
介绍关于收敛与不收敛的矢量场的概念，并强调其一些属性然后描述Mescheder等人文章提出的 consensus、optimization等方面的一些结论：在复杂的不收敛矢量场与理想的收敛矢量场之间进行插值
最后，正如我研究的期望那样，我还强调了另一个重要的细节，一个在文中没有讨论的：我们应该如何在小批量设置中做到所有这些？
简介：从GAN到矢量场
GANs可以被理解为博弈游戏（一个各不相互合作的双人游戏）。一个玩家控制θ并希望最大化其收益f（θ，φ），另一个控制φ并寻求最大化g（θ，φ）。当两个玩家都不再会通过改变参数来提高收益的时候游戏就达到了纳什均衡。因此，现在我们必须要设计一个算法来帮助达到这个纳什均衡。
但目前GANs似乎存在两个问题：
1.计算层面：纳什平衡（Nash equilibrium）达不到可能会退化。
2.算法层面：我们依然还没有找到可靠的工具来达到纳什均衡（即使我们现在的算法能很好的收敛到局部纳什均衡）。
Mescheder等在2017年非常成功地解决了第二个问题，为了找到纳什均衡，我们最好的工具是同步梯度上升算方法，一个由以下递归定义的迭代算法：
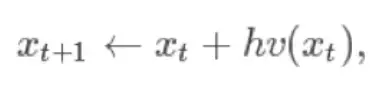
其中
是第t次迭代的结果,h是步长，v(x)是如下向量场:
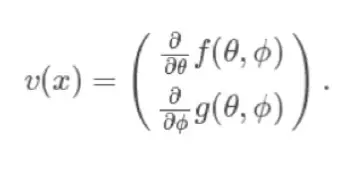
起初大家觉得这是一个重要的发现，可能看起来还挺矛盾的：将GANs训练视为神经网络训练的一个特殊例子是很自然的，但实际上它是另外一种方法。
同步梯度下降算法（simultaneous gradient descent）是梯度下降算法的概括，而不是特例。
不收敛的矢量场
普通梯度下降算法与同步梯度下降算法（simultaneous gradient descent）的一个关键区别在于，前者只能够收敛到向量场的固定点，后者可以处理不收敛的向量场。因此，我想花大部分在这篇文章里谈论这个差异以及这些术语是什么意思。
矢量场
是一个简单的函数，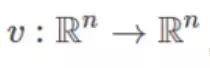
，输入为矢量
并输出具有相同维数的另一矢量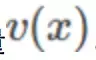
。
我们经常使用的矢量场是标量函数的梯度，例如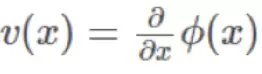
其中
可以是训练对象，能量或损失函数。这些类型的矢量场是非常特别的。它们被称为收敛的矢量场，可以简单的解释为“没有什么太复杂的因子”。标量函数的梯度和收敛的矢量场是一对一映射的：当且仅当向量v是收敛的时候，则存在标量φ的梯度等于v。
我们经常在机器学习中遇到的则是另一个种（但不经常将其视为矢量场）是由自动编码器定义的矢量场。 AE的输入一些向量x，并返回另一个相同大小的向量v（x）。比如在图5是Alain和Bengio在201年对2D数据的自动编码去噪声的矢量场训练，效果相当不错：
由AE定义的矢量场不一定是收敛的，这意味着可能会产生一些不确定性的奇奇怪怪的问题。会有什么样的奇怪的事情产生呢？让我们来看一个极端的例子：恒定卷积矢量场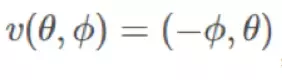
，这是一个非常典型的不收敛矢量场例子：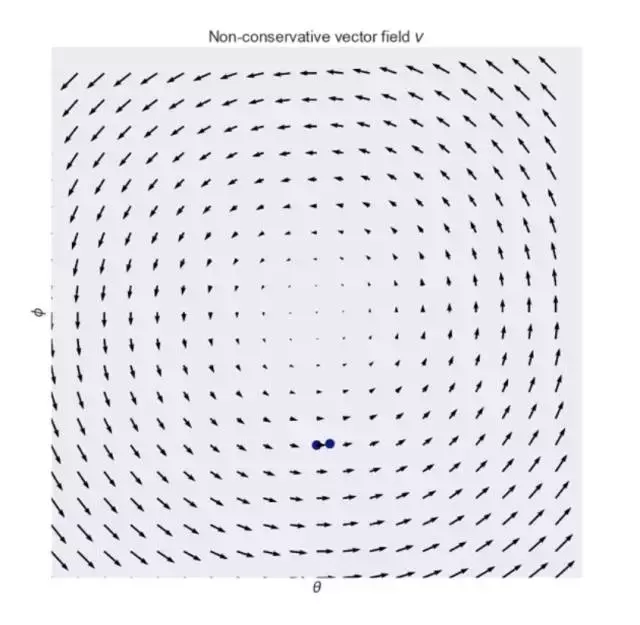
这个向量场在零和游戏中经常出现（译者注：zero-sum game就是指“零和博弈”，指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”，双方不存在合作的可能），其中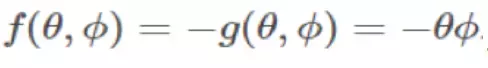
。这和Salimans等人在2016年论文“Improved Techniques for Training GANs”中第3节里面提到的对抗生成网络的框架里的一个小例子非常相似。如同在圆圈中的矢量场，可以很明显的看到它 场中的旋转。事实上，如果你沿着这个矢量场（同时这也是梯度下降的方向）的箭头，你最终会进入圈子里，如图所示：
请点击此处输入图片描述
可以把此矢量比作与埃舍尔的《不可思议城堡》（译者注：埃舍尔，荷兰 版画家，因其绘画中的数学性而闻名，有兴趣的可以看看《不可能存在的存在》：http://www.360doc.com/content/17/0705/08/27794381_668875548.shtml）。在埃舍尔的“不可能存在的城堡”中，仆人认为他们正在上台阶或者是在下台阶，但实际上他们所做的都是围绕着圈子。当然如果要将Escher的城堡构建成是一个真正的3D 模型则是不可能的。类似地，不可能将卷积矢量场表示为标量函数的梯度。
一个坏消息是，即使旋度场在
处具有平衡点，同步梯度下降算法也将永远发现不了。虽然我们我们共认梯度下降算法能在局部收敛到最小值，但是同步下降算法一般不能收敛到均衡点。它会陷入一个死循环，基于动量的变量甚至可以积累无限的动量直到完全崩溃。
一致优化方法（Consensus optimization）：训练一个不收敛的矢量场
Mescheder等人提出的解决方案是从原始构造一个收敛的矢量场，如下：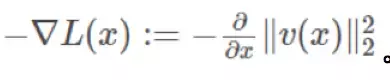
因为我们将它定义为标量函数L的梯度，这显然是收敛的。很容易看出，这个新的矢量场-∇L具有与v相同的固定点。下面我绘制了对应于上述旋度场的收敛矢量场-∇L：
这和我们之前熟悉的一样，L的梯度下降要收敛到局部最小值，即固定点v。现在的问题是，我们无法控制我们收敛到什么样的固定点。我们要寻求一个正平衡，但是-δL不能区分鞍点（既不是极大值点也不是极小值点的临界点）或平衡，或负平衡或正平衡之间。如下图说明了矢量场
在左侧的图片中，我注释了平衡点和鞍点。中间的图片说明了收敛松弛点L，其中鞍点和平衡都转向局部最小值。
那我们该怎么办？我们可以简单地采用原始v和它相关的-∇L进行线性组合，这种组合仍然是不收敛的矢量场看起来像旋度场（即上图第三个图片）。
通过这两个矢量场的组合，我们可能会得到一个稍微更好的模型，但仍然是不收敛的矢量场。衡量矢量场的效果的一种方法是查看其雅可比矩阵v'（x）的特征值。雅可比矩阵是矢量场的导数，对于收敛的矢量场，它被称为海森矩阵或二阶导数（译者注：关于雅可比矩阵和海森矩阵可以参阅网络资料——http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/）。与总是对称的海森矩阵不同，非收敛场的雅可比是非对称的，它可以具有复杂的特征值。例如旋度场的雅可比矩阵是
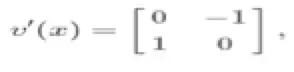
其特征值完全是虚构的+ i和-i。
Mesceder等人通过将v与-∇L线形组合，可以控制组合场的特征值（详见论文），如果我们选择足够大的γ，则同步梯度下降算法将收敛到平衡。这真的是太赞了（6666666）！
可悲的是，当我们增加γ时，我们也会像以前一样引入虚假的均衡。这里所谓的
平衡，其实际上只是v的鞍点。所以我们不能一味的关注γ，我们必须找到一个合理的中间地带。这是这种方法的局限性，目前尚不清楚实际中极限是多少。
再说说另一种方法：随机梯度方法的变种
我想再提一下这篇文章中没有讨论的一种方法，但是我认为对于任何想要达成一致优化效果的学者来说都是非常重要的：我们如何通过随机优化和小批量来实现的？虽然本文是在讲一般的应用场景，在对抗生成网络中，f和g实际上是数据点之间的一些回报的平均值，例如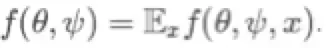
，这样对于L我们有如下表达式:
这样做的问题是，如何从一个样本中小批量的构建一个无偏差的估计量并不是一个简单的问题。在Jensen不等式中，上限是指简单的对每个数据点逐步的进行规范，然后平均将给出一个有偏差的估计。虽然在小批量处理的平均梯度计算标准中仍然存在偏差，但它可以更接近这个上限值。要构建一个无偏估计，我们可以使用以下表达式：
平均指标（average norm）和总体方差（population variance ）可以以无偏差的方式估计。 我已经和作者讨论过了，我会邀请他们发表评论，说明他们在实验中是如何做到的。 他们还承诺会在会议集影印版的论文中描述更多的细节。
总结
这篇论文让我开拓了视野，本来我一直认为在我们对抗生成网络中使用的梯度下降算法只是梯度下降的一种特殊情况，但实际上它只是是一个泛化，梯度下降的良好属性在这里并不能被认为是理所当然有的。希望这篇文章可以给大家带来一个对抗生成网络的满意答案。
